26.11.2023
Angle between intersecting straight lines - definition, examples of finding. Parallel Lines The angle between two intersecting lines is called
ASSESSMENT OF THE AMOUNT OF RISK AND CRITERIA FOR SELECTION OF A SOLUTION
Risk management is impossible without assessing its magnitude. The assessment method depends on the type of risk. Taking into account the variety of risks and the complexity of their management tasks, three types of assessments are used in practice: qualitative, axiological and quantitative. Qualitative risk assessment is widely used and allows...(Risks in accounting)
Intersecting lines
If straight lines intersect, then their projections of the same name intersect each other at a point that is the projection of the point of intersection of these lines. Indeed (Figure 2.30), if the point TO belongs to both lines AB And CD, then the projection of this point must be the intersection point...(Engineering graphics)
Crossing lines
Crossing straight lines do not intersect or parallel each other. Figure 2.32 shows two crossing lines general position: although projections of the same name intersect each other, their intersection points cannot be connected by a connection line parallel to the connection lines L"L" And...(Engineering graphics)
DISTANCE BETWEEN CROSSING STRAIGHTS
Distance between crossing lines A And Kommersant determined by the length of the perpendicular segment KM, intersecting both lines (and _1_ KM; Y.KM) (Fig. 349, b, c). The problem is solved simply if one of the lines is projecting. Let, for example, a±Pn then the required segment KM...(Descriptive geometry)
The relative position of a straight line and a plane, two planes
Signs of the relative position of a straight line and a plane, two planes Let us recall the signs of the relative position of a line and a plane, as well as two planes, familiar from stereometry. 1. If a line and a plane have one common point, then the line and the plane intersect (Fig. 3.6a). 2. If a straight line and a plane...(Fundamentals of Engineering Graphics)
Signs of the relative position of a straight line and a plane, two planes
Let us recall the signs of the relative position of a line and a plane, as well as two planes, familiar from stereometry. 1. If a line and a plane have one common point, then the line and the plane intersect (Fig. 3.6a). 2. If a line and a plane have two common points, then the line lies in the plane (Fig. 3.66)....(Fundamentals of Engineering Graphics)
In this article, we will first define the angle between crossing lines and provide a graphic illustration. Next, we will answer the question: “How to find the angle between crossing lines if the coordinates of the direction vectors of these lines in a rectangular coordinate system are known”? In conclusion, we will practice finding the angle between intersecting lines when solving examples and problems.
Page navigation.
Angle between intersecting straight lines - definition.
We will approach determining the angle between intersecting straight lines gradually.
First, let us recall the definition of skew lines: two lines in three-dimensional space are called interbreeding, if they do not lie in the same plane. From this definition it follows that intersecting lines do not intersect, are not parallel, and, moreover, do not coincide, otherwise they would both lie in a certain plane.
Let us give further auxiliary reasoning.
Let two intersecting lines a and b be given in three-dimensional space. Let's construct straight lines a 1 and b 1 so that they are parallel to the skew lines a and b, respectively, and pass through some point in space M 1 . Thus, we get two intersecting lines a 1 and b 1. Let the angle between intersecting lines a 1 and b 1 be equal to angle . Now let's construct lines a 2 and b 2, parallel to the skew lines a and b, respectively, passing through a point M 2, different from the point M 1. The angle between the intersecting lines a 2 and b 2 will also be equal to the angle. This statement is true, since straight lines a 1 and b 1 will coincide with straight lines a 2 and b 2, respectively, if a parallel transfer is performed, in which point M 1 moves to point M 2. Thus, the measure of the angle between two lines intersecting at a point M, respectively parallel to the given intersecting lines, does not depend on the choice of point M.
Now we are ready to define the angle between intersecting lines.
Definition.
Angle between intersecting lines is the angle between two intersecting lines that are respectively parallel to the given intersecting lines.
From the definition it follows that the angle between crossing lines will also not depend on the choice of point M. Therefore, as a point M we can take any point belonging to one of the intersecting lines.
Let us give an illustration of determining the angle between intersecting lines.
Finding the angle between intersecting lines.
Since the angle between intersecting lines is determined through the angle between intersecting lines, finding the angle between intersecting lines is reduced to finding the angle between the corresponding intersecting lines in three-dimensional space.
Undoubtedly, the methods studied in geometry lessons in high school. That is, having completed the necessary constructions, you can connect the desired angle with any angle known from the condition, based on the equality or similarity of the figures, in some cases it will help cosine theorem, and sometimes leads to the result definition of sine, cosine and tangent of an angle right triangle.
However, it is very convenient to solve the problem of finding the angle between crossing lines using the coordinate method. That's what we'll consider.
Let Oxyz be introduced in three-dimensional space (however, in many problems you have to enter it yourself).
Let us set ourselves a task: find the angle between the crossing lines a and b, which correspond to some equations of a line in space in the rectangular coordinate system Oxyz.
Let's solve it.
Let's take an arbitrary point in three-dimensional space M and assume that straight lines a 1 and b 1 pass through it, parallel to the crossing straight lines a and b, respectively. Then the required angle between the intersecting lines a and b is equal to the angle between the intersecting lines a 1 and b 1 by definition.
Thus, we just have to find the angle between intersecting lines a 1 and b 1. To apply the formula for finding the angle between two intersecting lines in space, we need to know the coordinates of the direction vectors of the lines a 1 and b 1.
How can we get them? And it's very simple. The definition of the direction vector of a straight line allows us to assert that the sets of direction vectors of parallel lines coincide. Therefore, the direction vectors of straight lines a 1 and b 1 can be taken as direction vectors 
And 
straight lines a and b respectively.
So, The angle between two intersecting lines a and b is calculated by the formula 
, Where And are the direction vectors of straight lines a and b, respectively.
Formula for finding the cosine of the angle between crossing lines a and b have the form 
.
Allows you to find the sine of the angle between crossing lines if the cosine is known: 
.
It remains to analyze the solutions to the examples.
Example.
Find the angle between the crossing lines a and b, which are defined in the Oxyz rectangular coordinate system by the equations 
And 
.
Solution.
The canonical equations of a straight line in space allow you to immediately determine the coordinates of the directing vector of this straight line - they are given by the numbers in the denominators of the fractions, that is, 
. Parametric equations of a straight line in space also make it possible to immediately write down the coordinates of the direction vector - they are equal to the coefficients in front of the parameter, that is, 
- direct vector . Thus, we have all the necessary data to apply the formula by which the angle between intersecting lines is calculated: 
Answer:
The angle between the given intersecting lines is equal to .
Example.
Find the sine and cosine of the angle between the crossing lines on which the edges AD and BC of the pyramid ABCD lie, if the coordinates of its vertices are known: .
Solution.
The direction vectors of the crossing lines AD and BC are the vectors and . Let's calculate their coordinates as the difference between the corresponding coordinates of the end and beginning points of the vector: 
According to the formula 
we can calculate the cosine of the angle between the specified crossing lines:
Now let's calculate the sine of the angle between the crossing lines: 
Parallel lines. Distance between parallel lines.
.
Corresponding angles
.
Internal and external crosswise angles
.
Internal and external one-sided corners .
Angles with correspondingly perpendicular sides
.
Proportional segments
. Thales's theorem.
Two straight lines AB and CD (Fig. 11) are called parallel, if they lie in the same plane and do not intersect, no matter how long they continue. Designation: AB || CD . All points of one parallel line are at the same distance from another parallel line. All lines parallel to one line are parallel to each other. It is generally accepted that the angle between parallel lines is zero. Angle between two parallel rays is equal to zero if they have the same directions, and 180° , if their directions are opposite. All perpendiculars ( AB, CD, EF , Fig. 12) to the same straight line K.M. parallelamong themselves. Reverse, direct K.M. , perpendicular to one of parallel lines, is perpendicular to the others. Length perpendicular segment between two parallel lines, There is distance between them.
When two parallel lines intersect with a third straight line, eight angles are formed (Fig. 13), which are called in pairs:
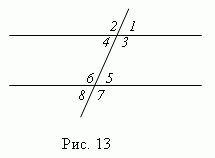
1) corresponding angles (1 And 5; 2 And 6; 3 And 7; 4 And 8 ); these angles are in pairs
are equal: ( 1 = 5; 2 = 6; 3 = 7; 4 = 8 );
2) internal crosswise angles (4 And 5; 3 And 6 ); they are pairwise equal;
3) external crosswise angles (1 And 8; 2 And 7 ); they are pairwise equal;
4) internal one-sided corners (3 And 5; 4 And 6 ); their sum is 180°
( 3 + 5 = 180
° ; 4 + 6 = 180 ° );5) external one-sided corners (1 And 7; 2 And 8 ); their sum is 180°
( 1 + 7 = 180° ; 2 + 8 = 180 ° ).
Angles with correspondingly parallel sides or equal to each other ( if they are both sharp or both dull, 1 = 2 , Fig. 14), or their sum is 180° ( 3 + 4 = 180°, Fig. 15).
The video course “Get an A” includes all the topics necessary for successful passing the Unified State Exam in mathematics for 60-65 points. Completely all problems 1-13 Profile Unified State Examination in mathematics. Also suitable for passing the Basic Unified State Examination in mathematics. If you want to pass the Unified State Exam with 90-100 points, you need to solve part 1 in 30 minutes and without mistakes!
Preparation course for the Unified State Exam for grades 10-11, as well as for teachers. Everything you need to solve Part 1 of the Unified State Exam in mathematics (the first 12 problems) and Problem 13 (trigonometry). And this is more than 70 points on the Unified State Exam, and neither a 100-point student nor a humanities student can do without them.
All the necessary theory. Quick ways solutions, pitfalls and secrets of the Unified State Exam. All current tasks of part 1 from the FIPI Task Bank have been analyzed. The course fully complies with the requirements of the Unified State Exam 2018.
The course contains 5 large topics, 2.5 hours each. Each topic is given from scratch, simply and clearly.
Hundreds of Unified State Exam tasks. Word problems and probability theory. Simple and easy to remember algorithms for solving problems. Geometry. Theory, reference material, analysis of all types of Unified State Examination tasks. Stereometry. Tricky solutions, useful cheat sheets, development of spatial imagination. Trigonometry from scratch to problem 13. Understanding instead of cramming. Clear explanations of complex concepts. Algebra. Roots, powers and logarithms, function and derivative. A basis for solving complex problems of Part 2 of the Unified State Exam.
